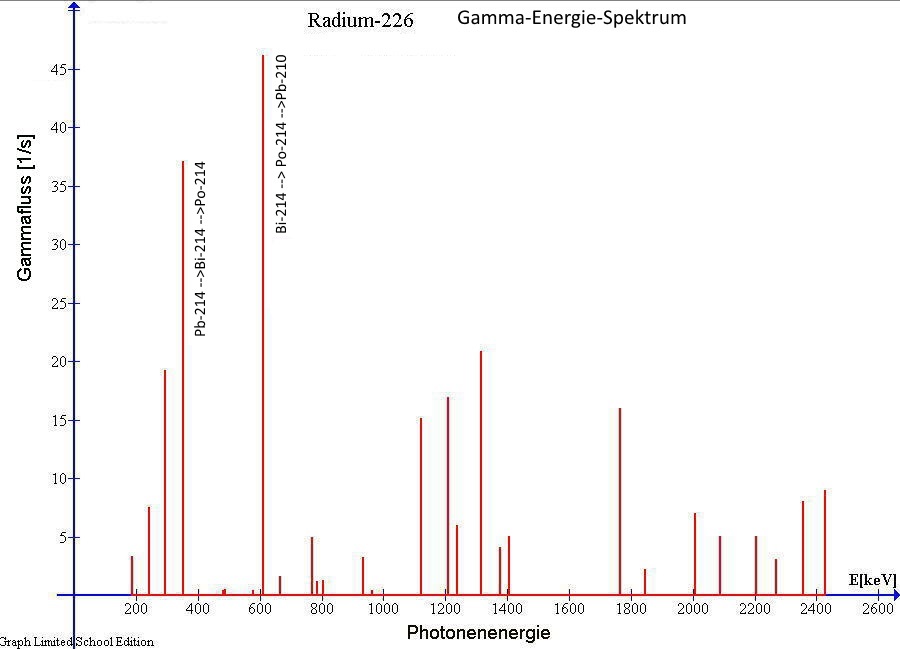
Bild01b : Gammaspektrum von Radium-226 (mit dem Gammafluss als interessierende Größe)
| Ein radiologischer Fingerabruck ist in dieser Terminologie identisch mit dem von einer einzigartigen Messapparatur an einer bestimmten Radioquelle gemessenes Impulshöhenspektrum. |
| Ein kostenloses Demo-Programm [1] , das aus einem Impulshöhenspektrum radioaktive Nuklide identifiziert, gibt es im WWW natürlich auch.... "Identify-Demo" zum [DOWNLOAD] |

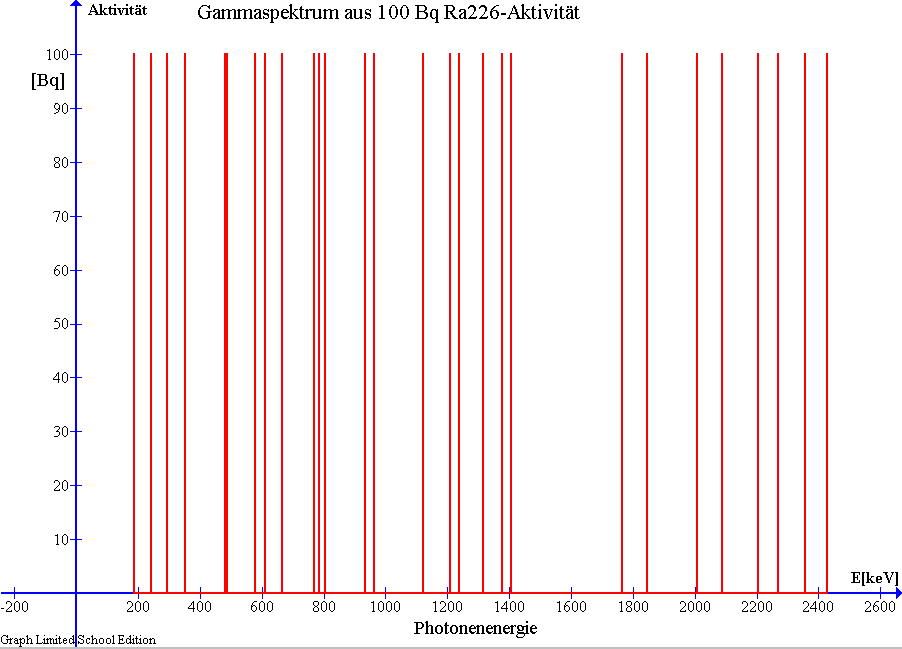
| Sind Materialeigenschaften und Bauweise der eingesetzten Messsonde grundsätzlich als Szintillator geeignet, und werden Impulshöhenspektren (radiologischen Fingerabdrücke) miteinander verglichen, welche ausnahmslos mit einem einzigartigen Versuchsaufbau von verschiedenen Radioquellen und unter Ausschluss systematischer Messfehler erzeut sind, dann haben Materialeigenschaften und die Bauart der Sonde keinen Einfluss auf Richtigkeit logischer Schlussfolgerungen welche aus Vergleichen von Impulshöhenspektren (radiologische Fingerabdrücke) hervorgehen. |
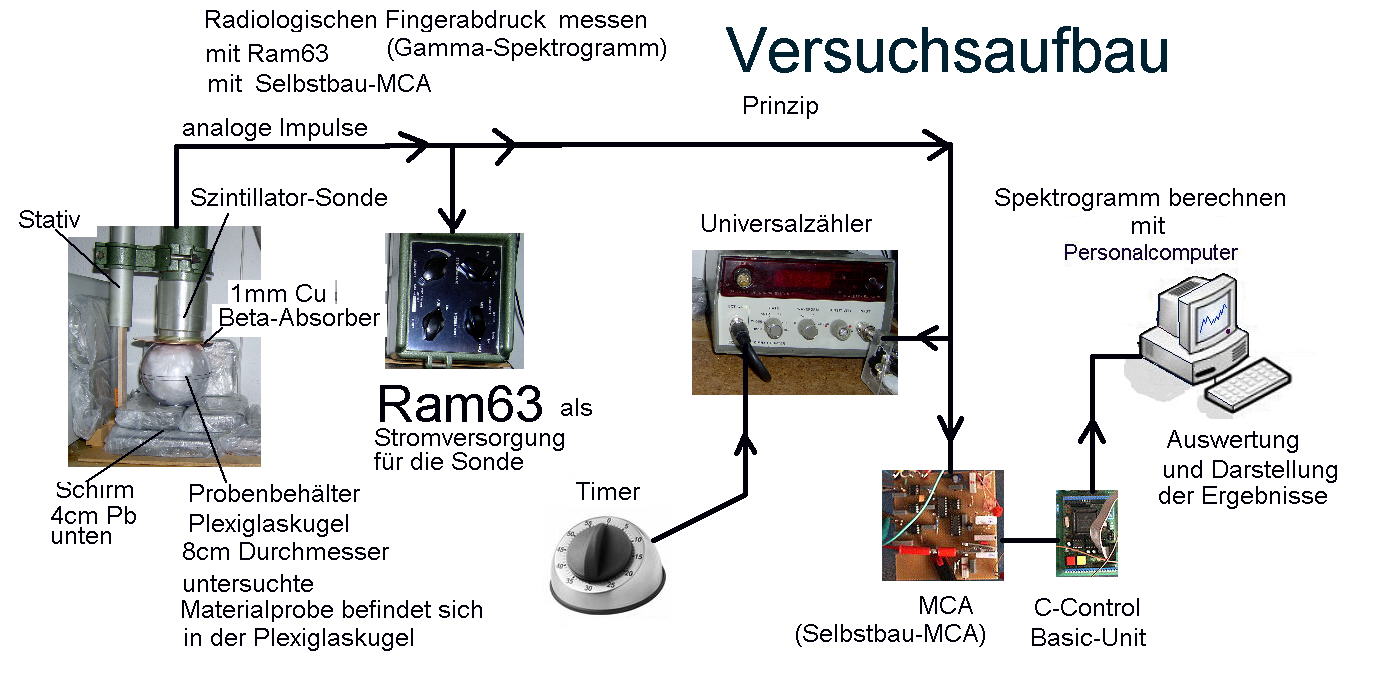
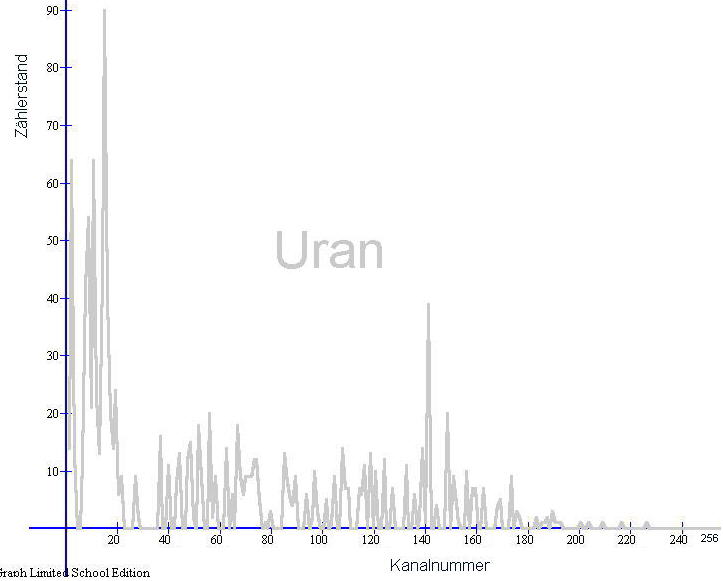
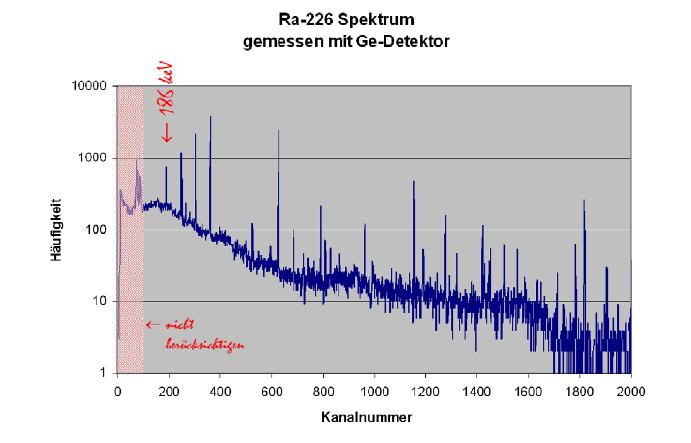
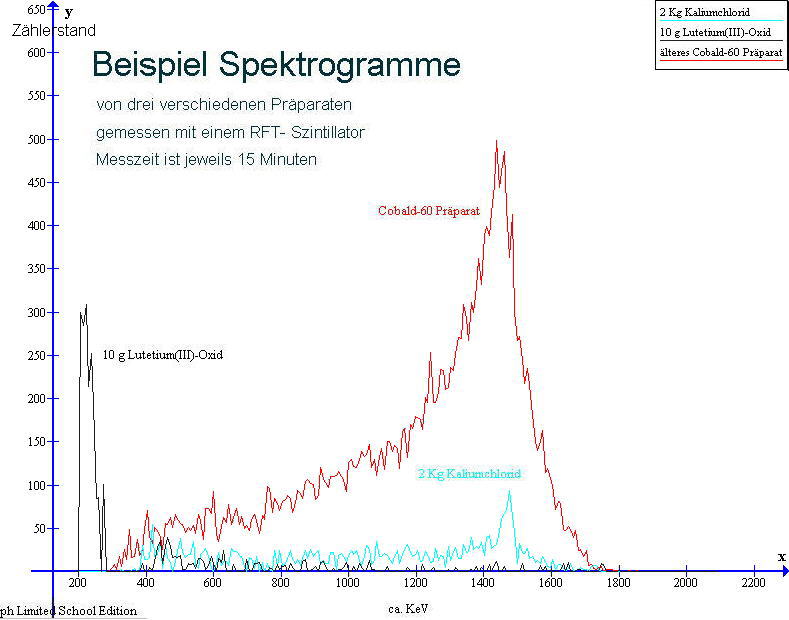
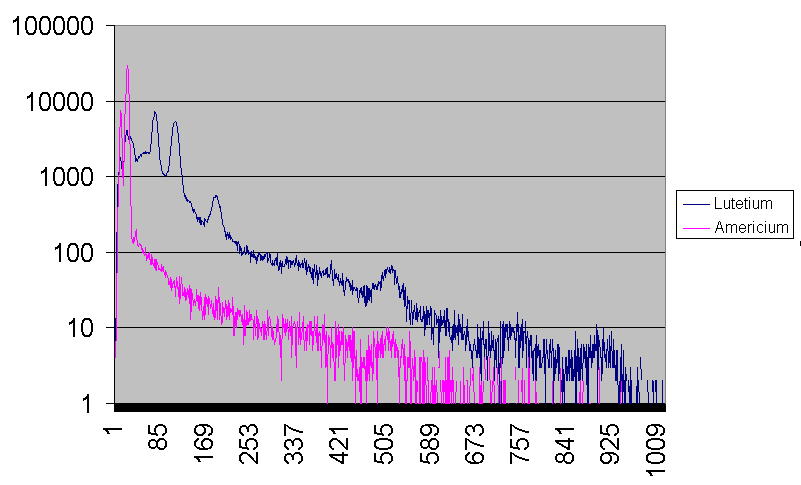
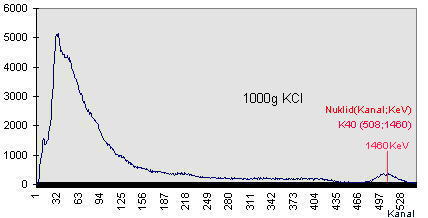
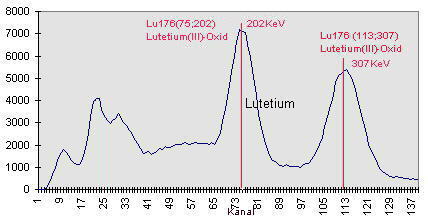
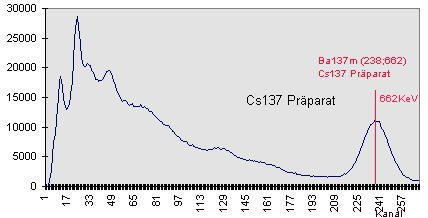
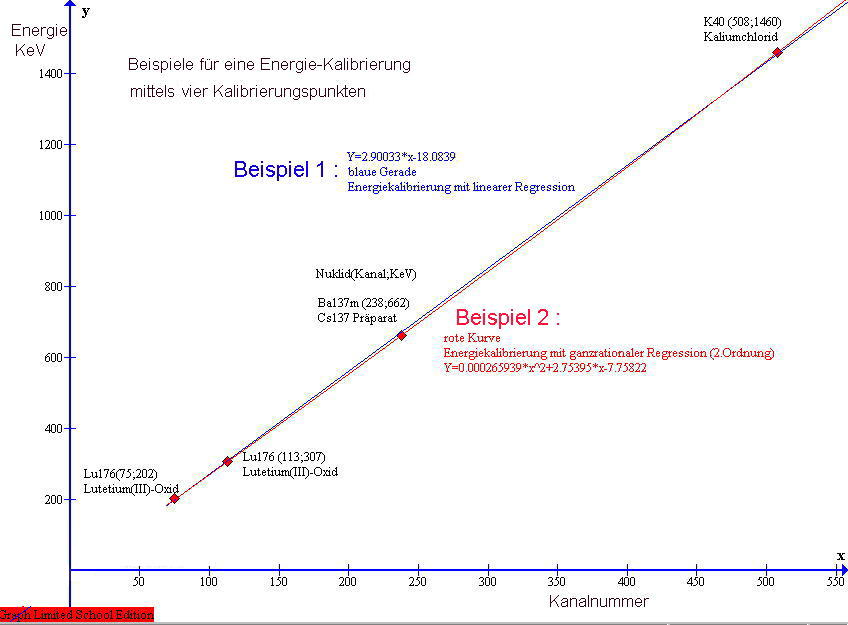
| Energiekalibrierung: Erwähnenswert ist noch, das ich eine näherungsweise Energiekalibrierung der Abszisse nun linear anhand spektraler Vergleiche mit Americium und Kaliumchlorid durchgeführt habe. Der eingesetzte MCA besitzt insgesamt 256 Kanäle und das Gerät erfasst Gamma-Strahlung zwischen nahe Null bis etwa 2,56 MeV. Die hier dargestellten Spektrogramme sind jedoch wegen qualitativer Materialeigenschaften des eingesetzten Szintillators keine sehr scharfen Gamma-Energie-Spektren. Deshalb lassen sich Nuklide nicht anhand scharfer Spektrallinien im Spektrogramm identifizieren. Zur Identifizierung von Nukliden möchte ich deshalb einen anderen Weg beschreiten. Die hier vorgestellte Methode zur Identifizierung von radioaktiven Nukliden in Stoffproben kommt grundsätzlich ohne Energiekalibrierung aus. Doch habe ich für eine verbesserte Anschaulichleit der dargestellten Spektrogramme die Abszisse in etwa auf Energie in keV justiert. Kanalnummer: Auf die Kanalnummer kann hier leicht zurückgerechnet werden. Diese ergibt sich aus dem auf der Abszisse ablesbaren Energiewert, dividiert durch Zehn. Beispiel : Kanalnummer 146 wurde hier zur Darstellung im Spektrogramm auf 1460keV umgerechnet. |
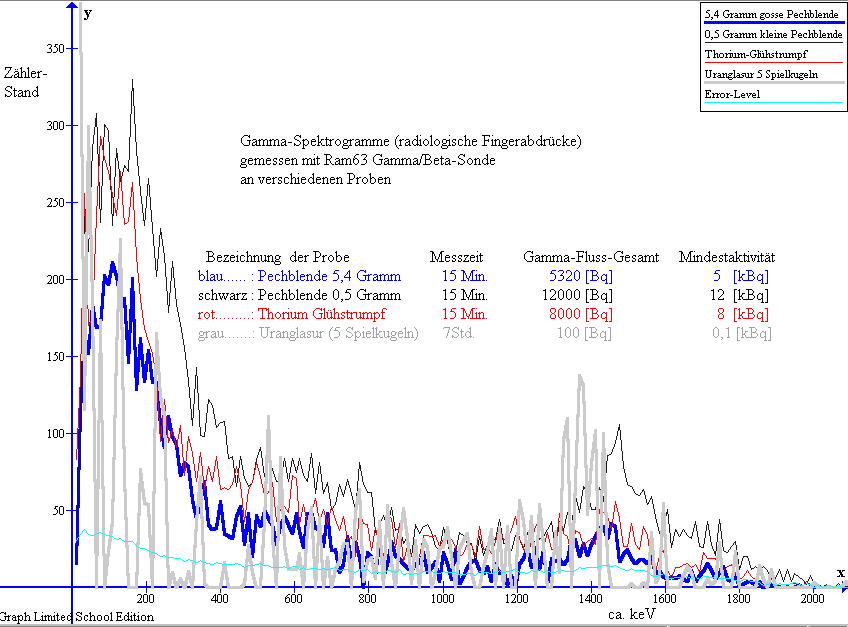
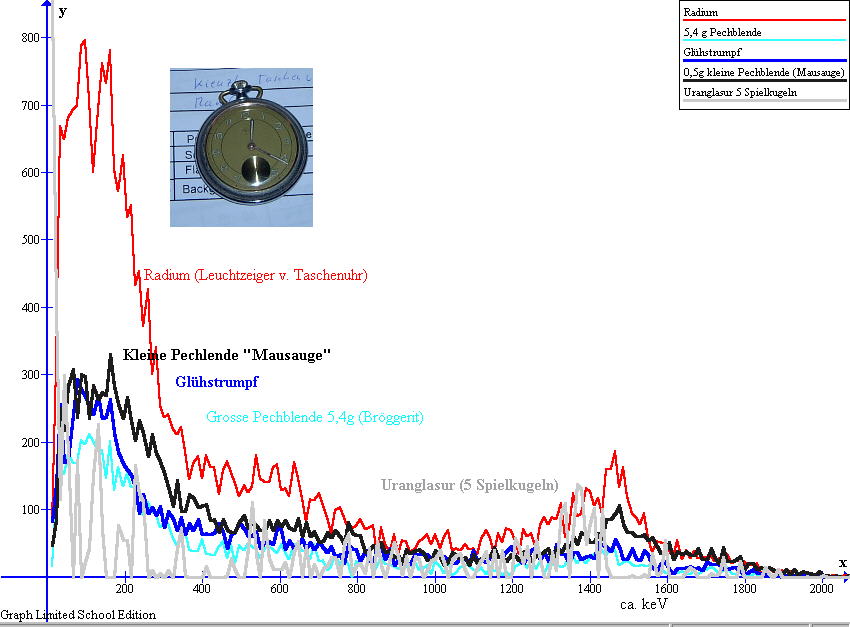
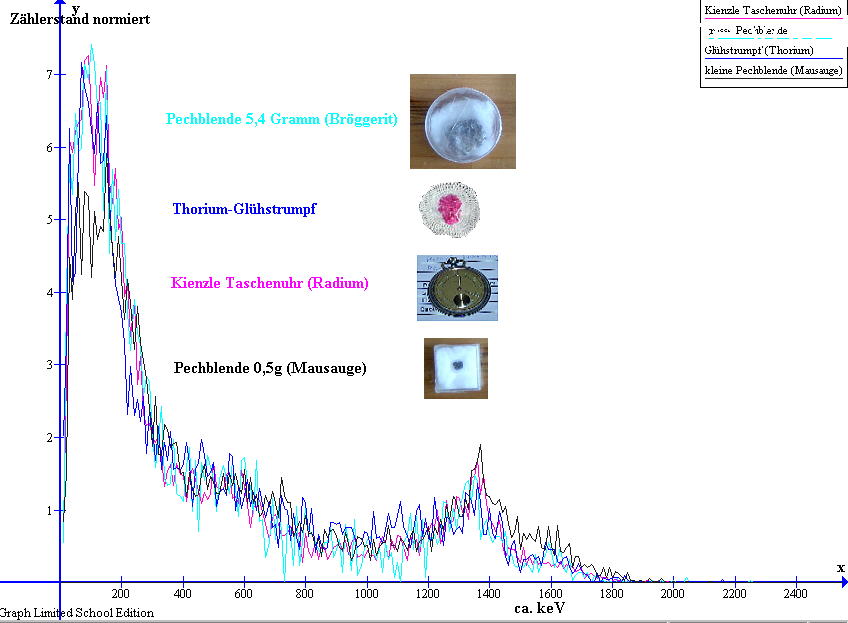
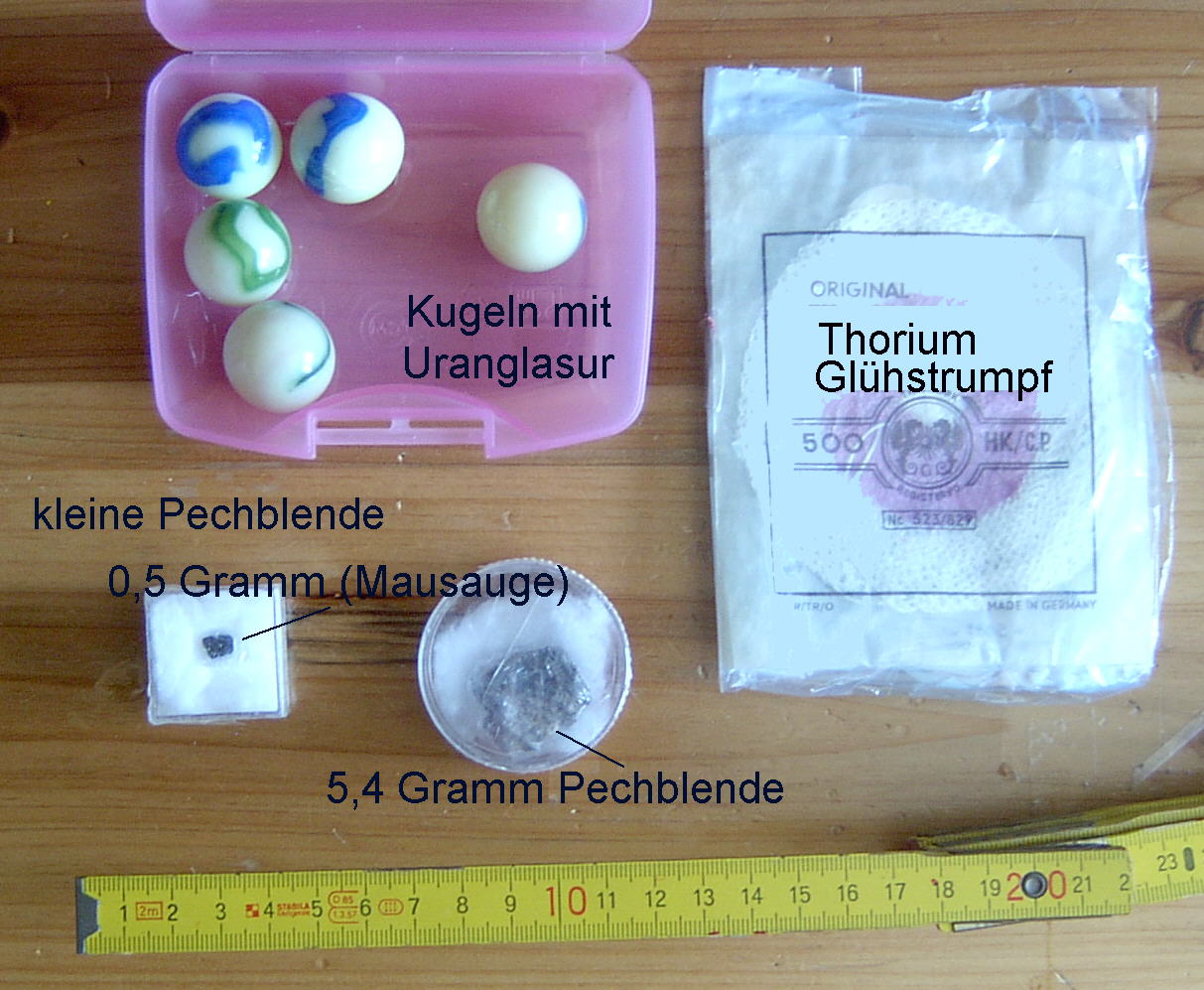
| Der sinnvolle Einsatz von Vergleichs- und Prüfstrahlern zur Nuklididentifikation hat u.a. Grenzen an der Vertrauenswürdigkeit betreffend Materialeigenschaften des als Prüfstrahler eingesetzten Produktes. |

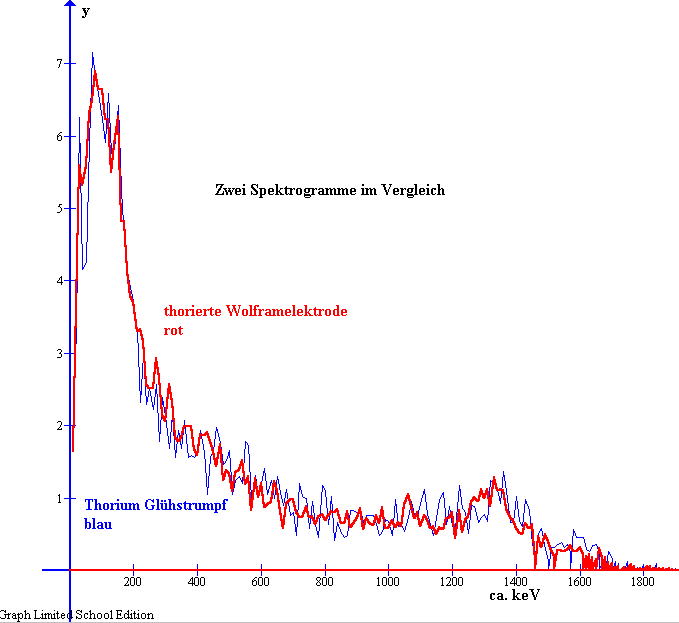
| Vergleiche per Augenschein sind
sehr mühsam. Deshalb möchte ich als numerisches
Maß
für den Grad
der Übereinstimmung einen Korrelationskoeffizient
heranziehen. Dies eröffnet mir numerische
Vergleichsmöglichkeiten per Computer. |

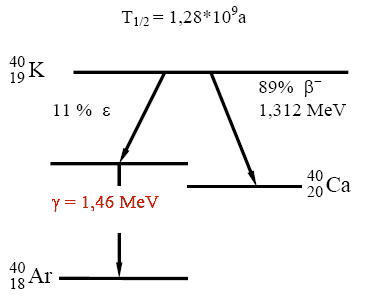
| Hinweis: Grafiken können im Firerfox-Browser bei Bedarf größer dargestellt werden mit Mouse-Klick rechts und "Grafik anzeigen" |