Der RFT-Szintillator, den ich bisher eingesetzt habe, stammt noch aus einem "Vor-Tschernobyl-Gerät". Für Messungen von Gamma-Spektrogrammen sind NaJ(Tl) Szintillatoren gebräuchlicher, als RFT-Szintillatoren.
Ein Gerät russischer Bauart liefert mir auch sofort einen fast neuwertigen NaJ(Tl)-Szintillator zusammen mit einem passenden Photomultiplier.
Links im Bild1 ist der NaJ(Tl)-Szintillator zu sehen, welcher auf den schwarzen Photomultiplier aufgesetzt ist. Die Elektronik, die im Bild noch rechts zu sehen ist, habe ich dann entfernt und den Photomultiplier zusammen mit dem Szintillator in ein eigenes lichtdichtes Gehäuse eingebaut. Dazu liefert ein regelbares Hochspannungsmodul welches ich mit einem Schaltkreis von Hamamatsu aufgebaut habe, die passende stabilisierte Hochspannung für den Photomultiplier. Die analogen Spannungsimpulse werden an der Anode des Photomultiplier entkoppelt und auf den Eigenbau- MCA geführt.
Für Messergebnisse, die später nachvollziehbar und vergleichbar sind, soll unbedingt die Konfiguration des Versuchsaufbaus einmal festgelegt werden. Diese Konfiguration wird dann für Messungen verschiedenster Proben beibehalten. Es hat sich eine Konfiguration mit einem liegenden oder senkrecht angeordneten Detektor und einer Materialprobe in Kugelform (8cm Durchmesser) bewährt. Zerkleinerte oder pulverförmige Materialproben lassen sich in einen Plastikbeutel füllen und selbst mit der Hand zu einer Kugel formen. Gut geeignet als Träger der Materialprobe sind auch kugelförmige Behälter (z.B. Halbhohlkugeln aus Metall oder Plexiglas).

Bild1a: Messaufbau mit liegend angeordnetem Detektor

Bild1b: Gamma-Spektrometer ; Messaufbau mit liegend angeordnetem Detektor ,
YB-Mini-MCA als Vielkanalzähler (Eigenbau)
Eine Plexiglaskugel beinhaltet die Materialprobe. Diese wird vor den Detektor platziert oder bei senkrechter Anordnung oben auf den Detektor gestellt. Der vordere Teil des Detektors kann bei einer liegenden Anordnung leicht mit einigen Bleibarren geschirmt werden. Durch die Schirmung mit Blei verringert sich die Nullrate und es verbessert sich die statistische Auswertbarkeit der Messergebnisse. Ist ein Kollimator vorhanden, kann dieser umgekehrt über den Detektor geschoben werden. Als Beta-Absorber dient eine 1mm starke Kupferscheibe, welche zwischen Detektor und Materialprobe platziert wird.

Bild1c: Gamma-Spektrometer Eigenbau; Beispiel für den
senkrecht angeordneten Detektor
(mit Kalibrierpräparat in einer Plexiglaskugel)
|
Formfaktor Manchmal
sollen Proben gemessen werden, welche eine 8cm
durchmessende Kugel nicht vollständig füllen. Andere
Probenmengen passen nicht
vollständig in dieses Kugelvolumen hinein. Um mit
Standardgeometrie
unterschiedliche Probenmengen messen zu können, kann also
entweder ein Teil von
zu großen Probenmengen für die Messung verwendet
werden oder es muss eine für
Standardgeometrie zu kleine Probenmenge durch radioaktiv neutrale
Füllstoffe so
auf das Volumen der Standardgeometrie gefüllt werden, das sich
eine
symmetrische (möglichst
homogene)
Verteilung der Aktivität innerhalb der Standardgeometrie
einstellt. In der
Praxis hat dies Nachteile, denn die zur Verfügung stehende
Probe muss in beiden
Fällen verändert werden. Es ist
wünschenswert, eine Materialprobe möglichst
unverändert auf den Detektor legen und messen zu
können. Pulverförmige
oder flüssige Proben lassen
sich leicht in einen Plastikbeutel füllen und zu einer Kugel
formen. Allerdings
hat bei verschiedenen Probenmengen die geformte Kugel häufig
einen anderen
Durchmesser, als die Kugel welche für die Standardgeometrie
gefordert ist. Eine
gut praktikable Möglichkeit unterschiedliche Kugeldurchmesser
auf die
Standardgeometrie umzurechnen bietet eine Umrechnung mittels Formfaktor. Der Formfaktor ist ein
Korrekturfaktor, mit
welchem multiplikativ die Messergebnisse welche mit
kugelförmigen Probenmengen
variabler Durchmesser gemessen wurden auf eine kugelförmige
Standardgeometrie
mit festem Durchmesser umgerechnet werden.
Es lässt sich zeigen, das für
Messergebnisse der spezifischen Aktivität,
der Formfaktor für kugelsymmetrische Probenmassen
näherungsweise gleich dem
Verhältnis zweier Kugeldurchmesser ist. |
Als erstes habe ich nun die Energiekalibrierung mit 10g Lu2O3 durchgeführt. Dabei stellt sich heraus, das diese russische Sonde aus technischen Gründen leider nur für Messungen bis etwa 700keV Photonenenergie nutzbar ist. Dafür erscheint dieser Messbereich jedoch sehr gut aufgelöst und das lässt mich auch sehr schöne Messergebnisse erwarten. Dadurch beflügelt komme ich mit den Kalibrierungen der russischen Sonde gut zurecht.
Mein Kalibrierpräparat besteht aus 10g Lutetium(III)-Oxid, aufgeteilt auf zwei kleine Glasbehälter mit jeweils 5g Lu2O3. Ich gebe das Lutetium(III)-Oxid symmetrisch verteilt in eine 8cm durchmessende Plexiglaskugel. Diese Plexiglaskugel habe ich als Frischhaltebehälter für Lebensmittel im Einzelhandel erworben. Sie ist in der Mitte teilbar. Zwischen den beiden Glasbehältern mit dem Lutetium(III)-Oxid, befindet sich ein Wattebausch. Dieser sorgt für die erforderliche Verteilung des Präparates innerhalb der Plexiglaskugel (siehe Bild1a bis Bild1c).
Lutetium(III)-Oxid hat laut Literatur (Test Adapters Based on Natural Lutetium) eine Aktivität von 45 Bq/Gramm. Die beiden Peaks bei 203keV und 307keV von Lutetium sowie die anhand der Literaturstelle bekannte Aktivität ermöglichen mir mittels Ausgleichfunktionen sowohl die Energiekalibrierung, als auch die Effektivitäs-Kalibrierung.
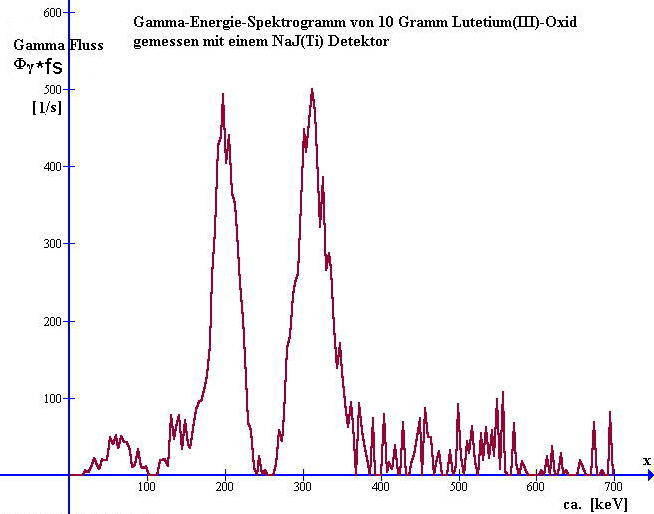
Das folgende Bild zeigt das Gamma-Energie-Spektrogramm (Impulshöhenspektrum) welches ich mit
dem
russischen Detektor an 10 Gramm Lutetium(III)-Oxid gemessen habe. Die
Messzeitspanne ist 60 Minuten.
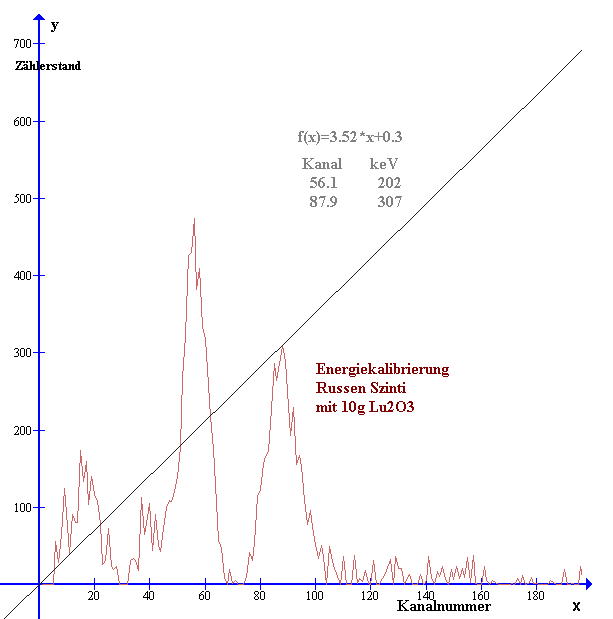
Bild1: Impulshöhenspektrum von 10Gramm Lu2O3 gemessen mit NaJ(Tl) Detektor
(60 Minuten Messzeitspanne)
Sehr schön sind die beiden Gamma-Energie-Peaks von Lutetium bei 203keV und 307keV Photonenenergie zu erkennen. Es lassen sich zwei Wertepaare (x | y) = (Kanalnummer | Photonenenergie) dieser Messanordnung ablesen. Aus den beiden abgelesenen Wertepaaren lässt sich eine Gradengleichung E=f(x) berechen, welche näherungsweise die Kanalnummer x auf die Photonenenergie E abbildet. Damit ist die Energiekalibrierung dieser Messanordnung durchgeführt. Die x-Achse der Spektrogramme wird nun mit den Energiewerten beschriftet.
Effektivitäts-Kalibrierung :
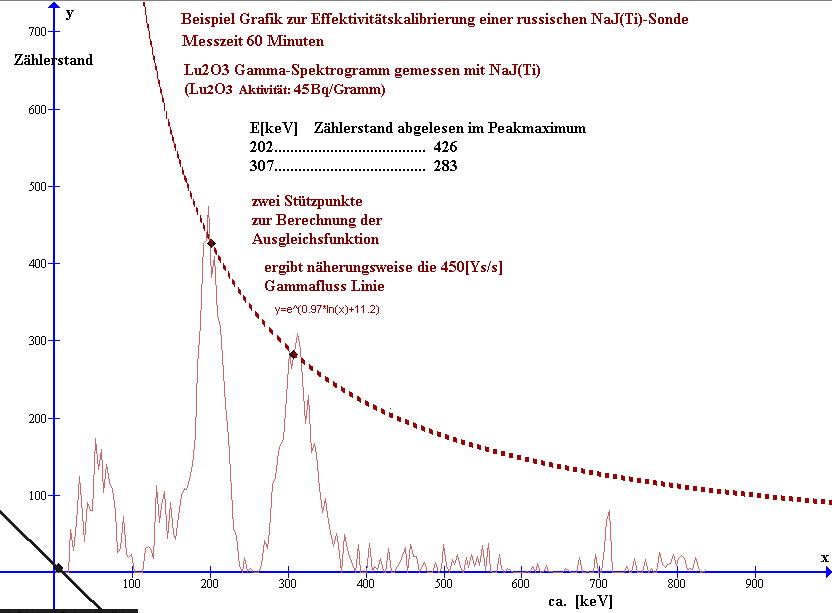
Bild2: Impulshöhenspektrum von Lu2O3 und
näherungsweise berechneter Verlauf des Ansprechvermögens in Abhängigkeit von der Photonenenergie
eines russischen NaJ(Tl)-Detektors (Beispielgrafik zur Effektivitätskalibrierung)
Aus der anschließenden Effektivitäts-Kalibrierung ergibt sich eine Ausgleichsfunktion y = eff(E). Diese beschreibt die Ansprechempfindlichkeit des Detektors als Funktion der Photonenenergie. Die Aktivität und das Zerfallsschema des Lutetium-Präparates (Kalibrierpräparat) ist aus der Literatur [4] bekannt und so kann zwischen den beiden Referenzen 203keV (84%) und 307keV (93%) mit einer Ausgleichsfunktion interpoliert werden. Außerhalb dieses Bereiches wird mit der selben Ausgleichsfunktion extrapoliert. Weil ich zwei Referenzen von dem Lutetiumpräparat für die Kalibrierung nutze, erhalte ich zwei Stützpunkte (Wertepaare) für die benötigte Ausgleichsfunktion.
Die beiden Wertepaare in diesem Beispiel (Bild2) sind:
(E | y)1 = (202 | 426)
(E | y)2 = (307 | 283)
Es wird wie folgt rektifiziert:
Y = ln(y) und X=ln(E) : Y = a+b*X
Die Parameter a und b lassen sich nun aus zwei Gradengleichungen durch einfache arithmetische Umformung bestimmen.
Das Beispiel liefert a=11,2 ; b=-0,97
Hier ist die Ausgleichsfunktion also : y = e(-0,97*ln(E)+11,2)
Nun werden alle weiteren
Messergebnisse auf diese Ausgleichsfunktion
bezogen,
womit dann die Anzahl der gezählten Impulse und die
tatsächlich von der Quelle
emittierten Anzahl Gamma-Quanten (Gammafluss) über
einen weiten
Energiebereich in ein konstantes Verhältnis gesetzt
ist. Verzerrungen
welche aufgrund physikalischer Eigenschaften des
Szintillators
entstehen, sind so in der grafischen Darstellung weitgehend
berichtigt. Auf diese Weise ist nun das Impulshöhenspektrum auf
das Gammaspektrum abgebildet und die Ordinate kann nun statt mit
"Zählerstand" mit der intreressierenden physikalischen
Grösse "Gammafluss" beschriftet werden.
An dieser Stelle stellt sich nun die Frage, ob die Ordinate auf Peakmaxima des
Kalibrierpräparates
zu justieren ist, oder ob auf die Peakflächen des
Kalibrierpräparates
justiert wird. Für eine einfache
Ablesbarkeit des Gammaflusses aus
dem Diagramm, habe ich mich dafür entschieden, die
Beschriftung der
y-Achse so zu justieren, das die
Peakmaxima geringfügig unterhalb (94%-93%) von 450 [1/s] Gammafluss fallen. Sind die Kalibrierungen sehr sauber und sorgfältig
durchgeführt, dann
erscheint nun im Gammaspektrum mit dem Gammfluss als interessierende
Größe von dem Lutetiumpräparat die Peakhöhe
bei 203keV geringfügig niedriger als
die Peakhöhe bei 307 keV. Ein beispielhaftes Ergebnis zeigt Bild3 :
Diese Vorgehensweise erfordert sehr viel Sorgfalt bei der Durchführung und ist sehr Aufwändig. Der Vorteil ist, das nun auch die Ordinate des Spektrogramms einen direkten Bezug zu einer physikalischen Größe hat.
Nun zum Abschluss habe ich natürlich auch die Waldpilzprobe, noch einmal mit meinen so kalibrierten russischen NaJ(Tl)-Detektor untersucht. Dazu gebe ich 60 Gramm der getrockneten Waldpilze gleichmäßig verteilt in die 8cm durchmessende Plexiglaskugel und messe diese mit dem hier ausführlich beschriebenen Versuchsaufbau. Das Ergebnis zeigt das folgende Bild:
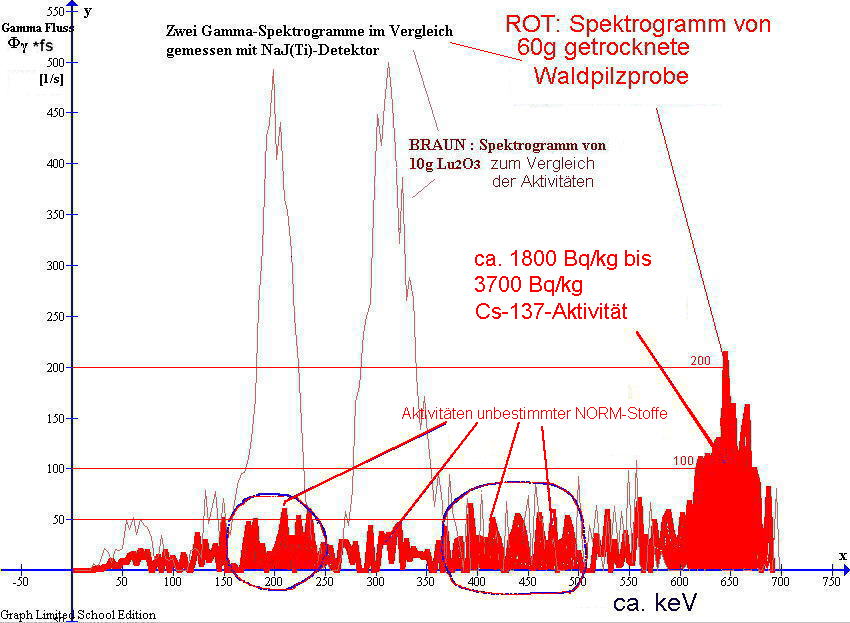
Bild4: gemessenes Gamma-Spektrum von 60g getrockneten Waldpilzen (rot)
im Vergleich mit dem gemessenen Gammaspektrum von 10g Lu2O3 (braun) ;
(jeweils gemessen mit meinem NaJ(Tl)-Detektor)
Im Spektrum Bild4 hebt sich um etwa 200keV sowie um 400keV bis 500keV und zwischen 600keV bis 700keV das Messergebnis der Waldpilze (roter Kurvenzug) deutlich vom Untergrund ab. Zur Abschätzung der Cs137-Aktivität suche ich zunächst das Peakmaximum im Energiebereich zwischen 600keV bis 700keV auf. Dieses lässt sich im Diagramm Bid4 zwischen 100 [1/s] bis 200 [1/s] ablesen (roter Kurvenzug). Ich dividiere durch die Probenmasse von 60 Gramm und multipliziere mit 1000. Das ergibt etwa 1600[1/s/kg] bis 3300[1/s/kg] Gammafluss aus der Probe mit ca. 662 keV Quantenenergie. Da eine Cs-137 Aktivität etwa zu 90% in Gamma-Strahlung umgesetzt wird, entsprechen 3300[1/s/kg] Gammafluss etwa 3700 Bq/kg spezifischer Cs-137 Aktivität.
Im unteren Spektralbereich bis etwa 500keV zeigen sich mehrere fast unauffällige Überhöhungen, welche nach meiner Interpretation auf Aktivitäten unbestimmter NORM-Stoffe oder TENORM-Stoffe deuten. Die Summe dieser spezifischen Aktivitäten unbestimmter radioaktiver Stoffe ist anhand der Ergebnisse schwer einschätzbar. Möglicherweise deuten die im Bild4 um 200keV erkennbaren Überhöhungen im Gamma- Spektrogramm der Waldpizprobe auf Radium-226. Aufgrund meines Verdachtes auf Radium-226 in dieser Probe gebe ich nun abschließend ein Beispiel zur Berechnung der Ra-226-Aktivität anhand Bild4. Der Gammafluss der Probe ist im Bild4 an der Stelle 186keV zu etwa Φγ*fs = 50 [1/s] ablesbar. Es wird auf 1Kg Probenmasse umgerechnet:
Φγ(186keV) = 50[1/s] / 60g *1000 = 833 [1/s/kg]
Ordne ich diesen Anteil Gamma-Strahlung dem radioaktiven Nuklid Ra-226 zu, dann errechnet sich die in der Pilzprobe enthaltene spezifische Aktivität allein von Ra-226 näherungsweise zu :
A = 883[1/s/kg] /5,4% = 16400 Bq/kg.
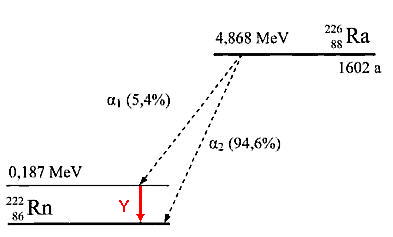
Den in diese Rechnung einzusetzenden Prozentanteil (5,4%) lese ich aus einem Zerfallsschema ab, welches der Literatur entnommen ist (siehe Bild5 [1]) Demnach setzt sich eine Ra-226-Aktivität etwa zu 5,4% in Gamma-Strahlung um.
Die Waldpilzprobe wurde auch von Herrn Andreas Öller mit seinem Eigenbau Spektrometer untersucht. Das mit dem weitaus hochwertigeren Messgerät erzeugte Spektrogramm hat eine noch feinere Auflösung und erstreckt sich über einen größeren Energiebereich. Das nächste Bild zeigt dazu eine Grafik mit Kanalnummern auf der x-Achse.
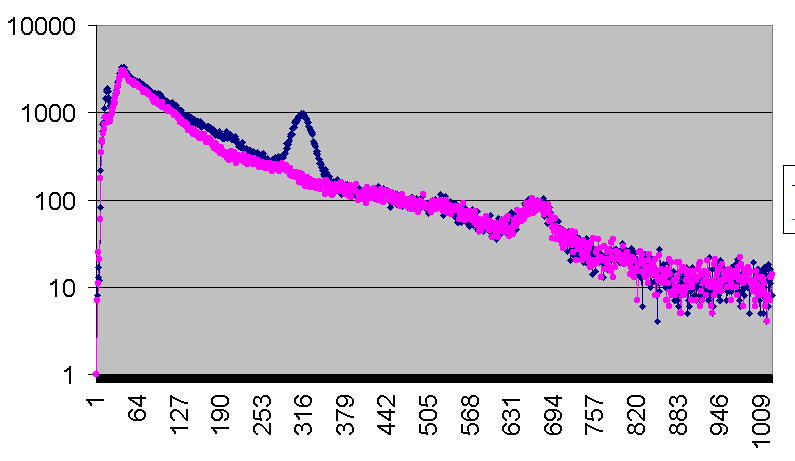
Bild6: Impulshöhenspektrum von 64g getrockneten Waldpilzen (blau)
und Impulshöhenspektrum vom Gamma-Hintergrund (rot)
95 Minuten gemessen mit Harshaw 2x2" NaJ(Tl) Detektor
jeweils 1204 Kanäle
Das Bild6 zeigt Abbilder der gemessenen Rohdaten. Auf der Abzisse ist der Wert für die Kanalnummer (Impulshöhe) aufgetragen und die Ordinate zeigt Zählerstände (Impulshäufigkeit). Der blaue Kurvenzug im Bild6 entspricht dem Impulshöhenspektrum von der Waldpilzprobe. Der rote Kurvenzug zeigt das Impulshöhenspektrum vom Hintergrund. Ereignisse aus radioaktivem Cäsium fallen hier auf Kanalnummer 311. Sehr deutlich ist genau an dieser Stelle im Spektrum das Abbild der Cs-137-Aktivität dieser Waldpilzprobe erkennbar. Bei genauem Hinblick sind im Bereich niedriger Kanalnummern tatsächlich auch in diesem Spektrogramm Bild6 weitere leichte Anhebungen gegenüber dem Hintergrund erkennbar, welche augenscheinlich auf Aktivitäten noch unbestimmter radioaktiver Stoffe deuten. Leider sind mir die überlieferten Rohdaten wegen fehlender Kalibrierinformationen nicht rektifizierbar. Ohne die erforderlichen Kalibrierdaten lassen sich diese beiden gemessenen Impulshöhenspektren leider nicht auf das Gammaspektrum abbilden.